Skip to content

Quick Start Guide

TL;DR

You can find a demonstration notebook here.

This guide will follow the steps necessary to get from model parsing to simulation. We will use a pre-defined config file (accessible in the repository) "MODELS/POST82.yaml".

Reading Model Configuration

The configuration files are parsed by the SymbolicDSGE.ModelParser class. The class provides a .get() method to return a ModelConfig object.

from SymbolicDSGE import ModelParser
from sympy import Matrix
from warnings import simplefilter, catch_warnings

model = ModelParser("MODELS/POST82.yaml").get()

with catch_warnings(): # (1)!
    simplefilter(action="ignore")
    mat = Matrix(model.equations.model)
mat
  1. Wrapping equations in a sp.Matrix is deprecated and used here solely for pretty-printing.

We've read the config and displayed the equations in a matrix:

\[ \left[\begin{matrix}\Pi{\left(t \right)} = \beta \Pi{\left(t + 1 \right)} + \kappa x{\left(t \right)} + z{\left(t \right)}\\x{\left(t \right)} = - \tau_{inv} \left(- \Pi{\left(t + 1 \right)} + r{\left(t \right)}\right) + g{\left(t \right)} + x{\left(t + 1 \right)}\\r{\left(t \right)} = e_{R} + \rho_{r} r{\left(t - 1 \right)} + \left(1 - \rho_{r}\right) \left(\psi_{\pi} \Pi{\left(t \right)} + \psi_{x} x{\left(t \right)}\right)\\g{\left(t \right)} = e_{g} + \rho_{g} g{\left(t - 1 \right)}\\z{\left(t \right)} = e_{z} + \rho_{z} z{\left(t - 1 \right)}\end{matrix}\right] \]

We can see that all variables are converted to SymPy objects (symbols/functions) and are accessible through the ModelConfig interface.

Compilation

In compilation, the symbolic model is projected into a functionalized and completely numeric form. Time-dependent variables are separated and equations are written as lambda objectives. Finally, the solver backend linearsolver is exposed to a single function representing all model equations.

from SymbolicDSGE import DSGESolver

solver = DSGESolver(model)
compiled = solver.compile(
    variable_order=None, # (1)!
    params_order=None, # (2)!
    n_state=3, # (3)!
    n_exog=2, # (4)!
)

print("Equations with symbols removed: \n", "\n".join(map(str, compiled.objective_eqs)))
print("\n")
print("Equations as passed to the solver: \n", compiled.equations)
  1. None | list[Function]. None uses the order in the config file.
  2. None | list[str]. None uses the order in the config file.
  3. Number of state variables (must be supplied)
  4. Number of exogenous variables (must be supplied)

At compilation, the equations are transformed as shown in the code output: 

Equations with symbols removed:
 -beta*fwd_Pi + cur_Pi - cur_x*kappa - cur_z
-cur_g + cur_x - fwd_x + tau_inv*(cur_r - fwd_Pi)
-cur_r*rho_r - e_R + fwd_r + (rho_r - 1)*(fwd_Pi*psi_pi + fwd_x*psi_x)
-cur_g*rho_g - e_g + fwd_g
-cur_z*rho_z - e_z + fwd_z


Equations as passed to the solver:
 <function DSGESolver.compile.<locals>.equations at 0x0000012D16AB5B20>

Variable Placement

The solver relies on the exogenous variables being placed in the first indices. You should ensure the first n_exog entries of the order correctly map to the exogenous variables. (either through the config or via the ordering)

Solution

The solution step takes steady-state values and optionally parameter calibrations to provide a SolvedModel.

from numpy import float64, array

sol = solver.solve(
    compiled,
    parameters=None, # (1)!
    steady_state=array([0.0, 0.0, 0.0, 0.0, 0.0], dtype=float64),
    log_linear=False,
)
print("Is stable: ", sol.policy.stab == 0)  # (2)!
print("Eigenvalues: ", sol.policy.eig)
  1. None | dict[str, float]. None uses the values in ModelConfig.calibration
  2. stable if sol.policy.stab == 0
Is stable:  True
Eigenvalues:  [0.27920118+0.j 0.83000003+0.j 0.84999992+0.j 2.56517116+0.j
 1.18470582+0.j] (1)
  1. Complex numbers are an artifact of linearsolve. All relevant matrices are cast to reals with np.real_if_close

Inspecting Model Dynamics

While we can check the matrices directly, we can also use the built-in methods SolvedModel.irf and SolvedModel.transition_plot to display the dynamics.

irf_dict = sol.irf(
    T=25,
    shocks=["g", "z"],
    scale=1.0,  # (1)!
    observables=True,  # (2)!
)
sol.transition_plot(
    T=25,
    shocks=["g", "z"],
    scale=1.0,
    observables=True,
)
irf_dict["z"] # (3)!
  1. shock = sig_var * scale
  2. Include observables in output.
  3. Path of the variable z.

This produces the outputs: transition_plot output

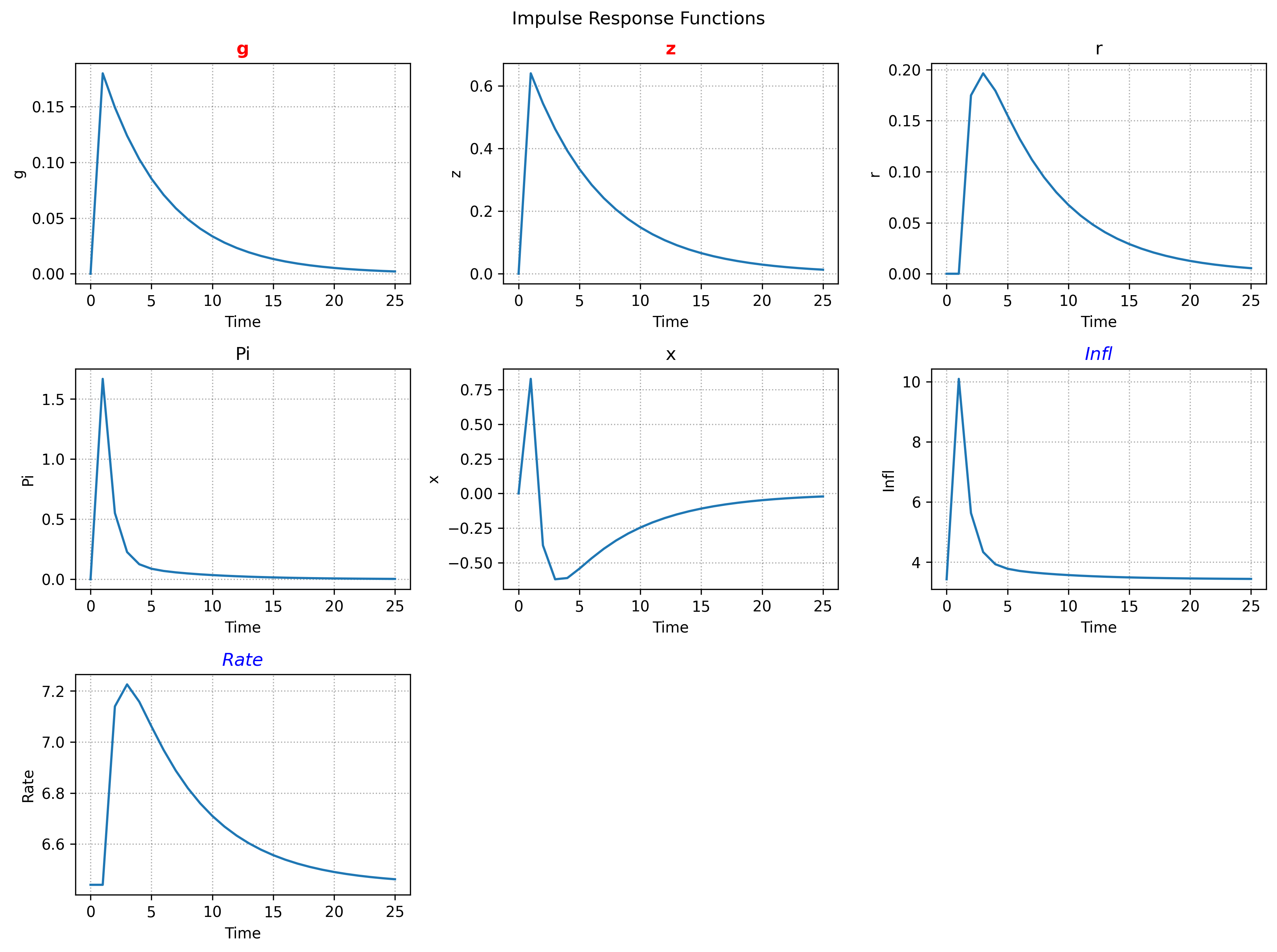
array([0.        , 0.64      , 0.54399995, 0.46239991, 0.39303989,
       0.33408388, 0.28397127, 0.24137556, 0.2051692 , 0.17439381,
       0.14823472, 0.1259995 , 0.10709957, 0.09103462, 0.07737942,
       0.0657725 , 0.05590662, 0.04752063, 0.04039253, 0.03433365,
       0.0291836 , 0.02480605, 0.02108514, 0.01792237, 0.01523401,
       0.01294891])

Simulation

SolvedModel also supplies a .sim() method for simulations. The method simulates T steps given an initial state array and a shock specification.

Shock specifications can take two basic forms.

  • A callable returning the complete shock array: Callable[[float | ndarray], ndarray]
  • A np.ndarray of innovations

Either specification is delivered to .sim in a dictionary corresponding to the variable the innovations are meant to effect. In case of multiple shocks with correlation the key for the dictionary uses "g,z" syntax. In correlated cases, the Callable option input should take a covariance matrix while the array option must be of shape (T, n_correlated_shocks). (order should match the dictionary key)

SymbolicDSGE.Shock is an interface simplifying the shock generation process. It can produce Callable generators for both univariate and multivariate shocks. The class has support for all SciPy distributions from the rv_generic and multi_rv_generic hierarchies. Alongside SciPy support, custom distributions implementing the .rvs method are supported through the pass-through of distribution args/kwargs.

from SymbolicDSGE import Shock

T = 200
shock_gen = lambda seed: Shock( # (1)!
    T=T,
    dist="norm",
    multivar=True,
    seed=seed, # (2)!
    dist_kwargs={ # (3)!
        "mean": [0.0, 0.0],
    },
).shock_generator() # (4)!

sim_shocks = {
    "g,z": shock_gen(seed=1) # (5)!
}
  1. Notice the seed argument to the class being parametrized through a lambda. This step is not necessary for functionality. It saves the code of declaring two instances with different seeds if two shocks share distributions.
  2. Seed is passed through here, the code below would operate the same if we used seed=1 instead of using a lambda.
  3. The kwargs specified here are passed to the distribution object in the backend (to SciPy's rvs methods in this case)
  4. shock_generator produces the Callable object from the parameters given at class initialization. The methods either accept a float sig or a covariance matrix cov created inside the .sim method.
  5. The value in this pair is a standalone function that does not depend on model parameters. Once created it can be reused across simulations; the appropriate sig or cov is constructed internally from model parameters at simulation time.

shock_gen() returns a callable that .sim uses in the simulation loop to produce shocks. With the shocks produced, we can simulate stochastic paths as follows:

import pandas as pd

sim_data = sol.sim(
    T=T,
    x0=array([0.0, 0.0, 0.0, 0.0, 0.0], dtype=float64),  # (1)!
    shocks=sim_shocks,
    shock_scale=1.0,
    observables=True,
)
del sim_data["_X"]  # (2)!
pd.DataFrame(sim_data).head(10)
  1. Simulation starts at steady state
  2. "_X" is a ndarray of all non-observable states for each time t. It is deleted here for code brevity in producing a DataFrame.
g z r Pi x Infl Rate
0 0 0 0 0 0 3.43 6.44
1 0.0113 1.0502 0 2.0097 0.4527 11.469 6.44
2 -0.2055 0.5741 0.205 -0.4441 -1.6807 1.6538 7.2601
3 -0.4925 1.0832 0.1083 0.2587 -1.8046 4.4646 6.873
4 -0.4139 2.0507 0.0962 2.3427 -1.0963 12.8009 6.8249
5 -0.3628 1.9517 0.3014 1.2818 -2.2254 8.557 7.6456
6 -0.5415 2.6315 0.3544 1.8491 -2.8505 10.8264 7.8577
7 -0.5357 2.0374 0.4482 0.2843 -3.6404 4.5671 8.233
8 -0.5484 2.477 0.362 1.503 -2.9801 9.442 7.8881
9 -0.6129 2.0109 0.4187 0.1822 -3.7172 4.1587 8.1148

Alternative to a DataFrame, we can also plot the simulated paths:

from numpy import ceil, sqrt
import matplotlib.pyplot as plt

fig_square = ceil(sqrt(len(sim_data))).astype(int)
size = (4 * fig_square, 3 * fig_square)
fig, ax = plt.subplots(fig_square, fig_square, figsize=size)
ax = ax.flatten()

while len(ax) > len(sim_data):
    fig.delaxes(ax[-1])
    ax = ax[:-1]

for i, (var, path) in enumerate(sim_data.items()):
    ax[i].plot(path)
    ax[i].set_title(var)
    ax[i].grid(linestyle=":")
plt.suptitle(f"Simulation over {T} periods with stochastic shocks", fontsize=16)
plt.tight_layout()
Simulation Plots

Further Steps

This guide covers the basic capabilities and usage of SymbolicDSGE. Further tools include:

  • SymbolicDSGE.FRED for easy U.S. macro data retrieval
  • SymbolicDSGE.math_utils for basic detrending, HP filters, etc.
  • SymbolicDSGE.KalmanFilter for a one-sided Kalman Filter implementation. (standalone as of now but easy model integration interface will be developed)

If you've read to this point and would like to inspect/interact with the code this guide refers to, you can visit this link to the file.

Download Guide Notebook